基本概念
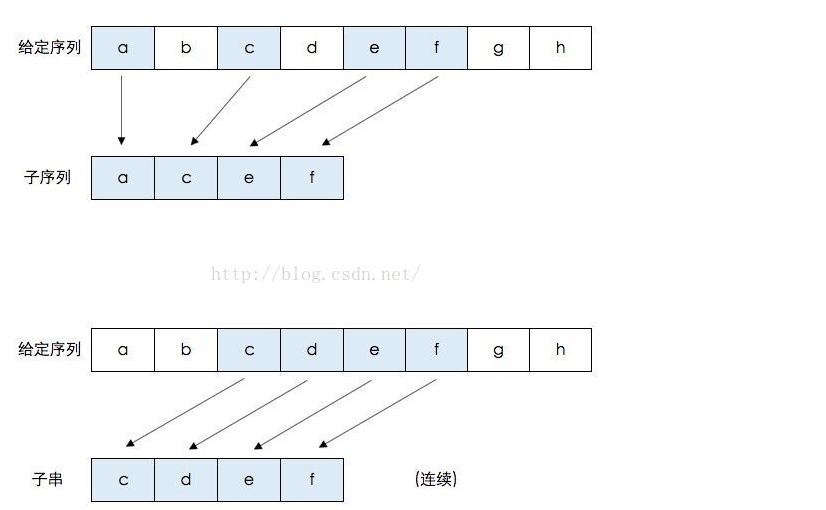
最长公共子序列和最长公共子串不同
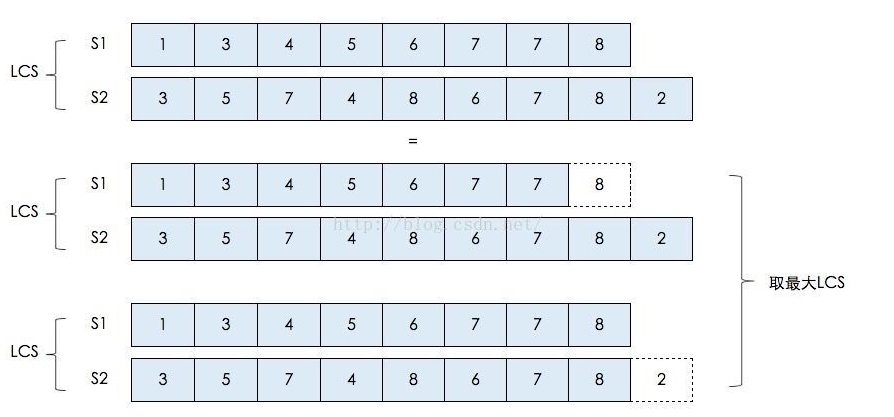
递归原理
递归公式
假设我们用c[i,j]表示Xi 和 Yj 的LCS的长度(直接保存最长公共子序列的中间结果不现实,需要先借助LCS的长度)。其中X = {x1 … xm},Y ={y1…yn},Xi = {x1 … xi},Yj={y1… yj}。可得递归公式如下: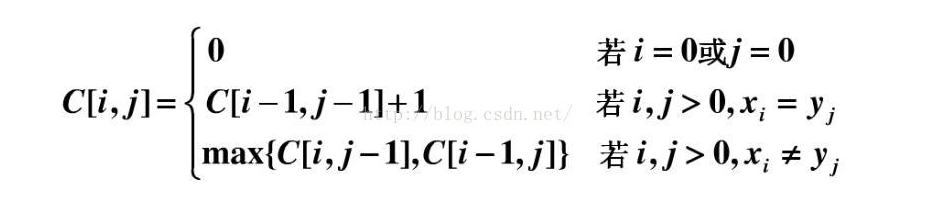
案例推导
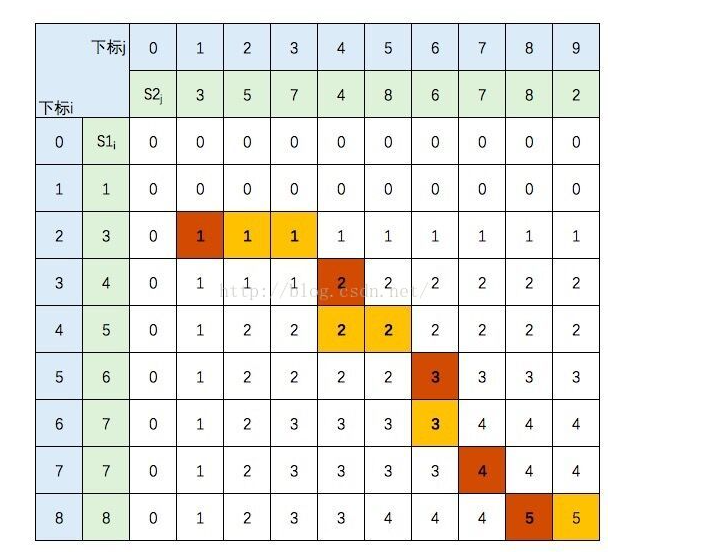
最长公共子序列 LCS解法
其中最长的公共子序列长度为dp[n][m]
1 | class Solution { |
better tomorrow


假设我们用c[i,j]表示Xi 和 Yj 的LCS的长度(直接保存最长公共子序列的中间结果不现实,需要先借助LCS的长度)。其中X = {x1 … xm},Y ={y1…yn},Xi = {x1 … xi},Yj={y1… yj}。可得递归公式如下: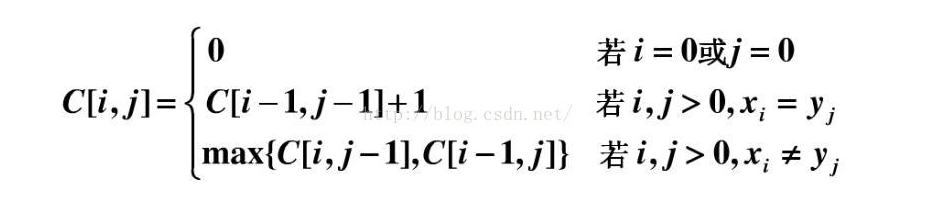

其中最长的公共子序列长度为dp[n][m]
1 | class Solution { |